二 次 関数 の グラフ 頂点
feh 雷 の ブレス【3分で分かる!】二次関数の頂点の求め方をわかりやすく . 二次関数の頂点の求め方 その1. では具体的に二次関数の頂点を求めてみましょう。 一つ目の求め方は、 平方完成をして頂点を求める方法 です。 平方完成について復習したい場合はこちらの記事を参照してください。 【3分でわかる! 】平方完成のやり方のコツ. 2017.05.13. 具体例を挙げます。 例題. 二次関数 y = x2 + 4x + 10 の頂点の座標を求めよ。 例題の解答・解説. 平方完成をします。 y = (x + 2)2 − 4 + 10. y = (x + 2)2 + 6. 二次関数の軸と頂点の求め方など | 高校数学の美しい物語. 二次関数の軸と頂点を求める公式. 二 次 関数 の グラフ 頂点さきほどの例題で見たように,平方完成すれば軸と頂点がわかります。 一般の場合にやってみると以下の公式が得られます。 軸と頂点を求める公式. 二 次 関数 の グラフ 頂点2次関数のグラフの書き方・頂点・平行移動について全て語った . 2次関数の頂点と軸の求め方 ⋯「( y=ax^2+bx+c )」のグラフは「( y=a(x-p)^2+q )」の形に変形することで、軸と頂点がわかる。 ( y=a(x-p)^2+q ) のグラフ ⋯( y=ax^2 ) のグラフを( x ) 軸方向に ( p )、( y ) 軸方向に ( q ) だけ平行移動したグラフになる。. 二次関数グラフの書き方&頂点を一発で求める方法とは . 二次関数のグラフの書き方は、主に4ステップです! 【手順1:平方完成をする】 まずは、グラフを書きたい二次関数を平方完成します。 ※平方完成のやり方がわからない人は、 平方完成のやり方について詳しく解説した記事 をご覧ください。 y=x 2 -4x-12を平方完成すると、 y= (x-2) 2 -16となりますね。 【手順2:頂点を求める】 平方完成して、y= (x-p) 2 +qの形に変形できれば、頂点を求めましょう。 y= (x-p)2+qのグラフの頂点の座標は、 (p,q)となります。 ※二次関数の頂点について深く学習したい人は、 二次関数の頂点について詳しく解説した記事 をご覧ください。 したがって、先ほど平方完成した. 二 次 関数 の グラフ 頂点【2次関数】グラフの頂点・軸の求め方はこれだけ!【練習問題 . 2次関数のグラフの頂点と軸はどうやって求めたらいいの? 2次関数の頂点・軸の公式は覚える必要があるの? 簡単に素早く求める方法を知りたい!. 二次関数のグラフの書き方とは?【頂点・軸・共有点の求め方 . 二次関数 $y=ax^2+bx+c$ のグラフの書き方は、以下の $4$ ステップを押さえればOKです。 まず平方完成をする。 頂点の座標を求める。. 境界 の rinne 苺
草薙 な すべ え軸と頂点ってなに?2次関数のグラフのかき方 | すうがくのいえ. 軸と頂点ってなに? 2次関数のグラフのかき方. 二 次 関数 の グラフ 頂点5月 29, 2023. 数の関係性のことを 関数 と呼んで、関数はグラフに表すことができる。 なので、2次関数もグラフに表すことができる。 結論から言うと、 「凸の向き」「頂点」「y切片」 の3つが分かれば2次関数をグラフに表せる。 ってか、 そもそも2次関数ってなんだっけ? 2次関数ってなんだっけ? 2次関数 は 2次式の関数 っていう意味。 2次式 とは、 最も次数の高い項の次数が「2」の式 ということ。 基本的に2次関数は y = a x 2 + b x + c ( a, b, c は定数、 a ≠ 0 ) って表す。 例えば「 y = x 2 + 2 x + 1 」とか「 y = x 2 + 4 x − 5 」のこと。. 二次関数のグラフの書き方と、頂点・軸・切片の求め方 | 受験辞典. まずは、二次関数のグラフを書くのに必要な次の情報を集めます。 放物線の頂点と軸 グラフの向き 軸との交点 次のステップで求めていきます。. 二 次 関数 の グラフ 頂点二次関数の頂点とは?軸とは?公式や超重要問題も徹底解説!. 二次関数の頂点を求める方法は2つあります。 方法その1:平方完成を使う. y=ax 2 +bx+cという二次関数があったとき、y=ax 2 +bx+cを平方完成するとy=a(x-p) 2 +qになる場合、頂点は(p、q)となります。 例えば、y=x 2 +8x+10という二次関数があったとします。 y=x 2 +8x+10を平方完成するとy=(x+4) 2 -6ですね。 ※平方完成のやり方がわからない人は、 平方完成の公式・やり方について解説した記事 をご覧ください。. 二次関数のグラフの書き方を3ステップで解説!. 二次関数のグラフは頂点の座標とy軸との交点を滑らかに結ぶことで描くことができます。本記事では、二次関数のグラフの書き方を簡単な3つの手順で書けるように解説しています。. 二次関数のグラフと問題の解き方!覚えておくべき2つの公式. 二 次 関数 の グラフ 頂点という二次関数のグラフの頂点の座標は(p、q)である、とされます。 上記で示したグラフ「 y=x² 」は. 二 次 関数 の グラフ 頂点y=x². y=(x-0)²+0. と表現することもできますね。 したがって、頂点は(0,0)であると読み取ることができるのです。 二次関数の問題について. 二 次 関数 の グラフ 頂点前項では、シンプルに当該二次関数が原点を頂点とする場合について考えましたが、むしろこれは極めて例外的な場面でしょう。 もっとも、中学数学では、二次関数が原点を頂点としない場合が問われることは少なく、先の一般式「y=a(x-p)²+q 」を利用しなければならない場面は極めて限定的であるとも言えます。. 二次関数のグラフの作成方法を図解で解説!分数があるときの . 手順1:頂点の座標を求める. 手順2:y切片を求める. 手順3:軸で左右対称になるようにグラフを書く. 二次関数の式に分数が含まれているときのグラフの作成方法. 二次関数のグラフの作成(練習問題) 二次関数のグラフ作成にあたっての事前知識. まずは二次関数のグラフを作成するにあたっての事前知識をご紹介します。 まず、 二次関数のグラフは必ず放物線状になります。 一次関数のように直線になることはありません。 ※ 一次関数とは何かについて解説した記事 もご用意しているので、ぜひ参考にしてください。 そして、 y=ax2+bx+cという二次関数があるとき、a>0ならばグラフは以下のように谷形の形状になり、これを下に凸と言います。 ※凸は「とつ」と読みます。. 【3分で分かる!】2次関数のグラフの描き方をわかりやすく . 二次関数のグラフが上に凸か下に凸か調べるのは非常に簡単で、y = ax2 + bx + cのx2の係数aが正ならば下に凸、負ならば上に凸です。 具体的に言うと、 y = x2 + 2x + 3 は x2 の係数が 1 で、これは正なので下に凸です。 y = −3x2 + x − 4 は x2 の係数が −3 で、これは負の数なので上に凸となります。 どっちがどっちか忘れてしまったら、 y = x2 のグラフを思い出してください。 これはグラフの形からして下に凸ですね。 y = x2はx2の係数1が正なので、x2の係数が正なら下に凸だと分かります。 二次関数のグラフの描き方②:平方完成する. 二次関数の軸・頂点の求め方を解説!平方完成ができればok . 2次関数の軸や頂点は以下の形で求めることができます。 2次関数の軸・頂点. 二 次 関数 の グラフ 頂点2次関数 y = a(x − p)2 + q において、 放物線の軸: x = p. 頂点の座標: (p, q) また、 2次関数の頂点の求め方は主に2つ あります。 平方完成で求める方法. 公式に代入する方法. 二 次 関数 の グラフ 頂点本記事では 2次関数の軸と頂点の求め方を解説 します。 平方完成が苦手な方も本記事を参考に平方完成をマスターして、二次関数の軸と頂点を求められるようになりましょう。 目次. 二 次 関数 の グラフ 頂点1 2次関数の軸と頂点. ママ 友 若妻 たち の 中出し 危機 一髪 ゲーム
牡 羊 座 と 牡 羊 座 の 相性2 頂点と軸の求め方. 3 分数やマイナスを含む2次関数. 4 おすすめの動画. 5 軸・頂点を求める《練習問題》 6 軸と頂点 まとめ. ※本ページは学習アプリのプロモーションが含まれています。 シータ. 2次関数のグラフ・軸・頂点・平行移動・対称移動 | 数学の . 二 次 関数 の グラフ 頂点2次関数のグラフ・軸・頂点・平行移動・対称移動 | 数学の偏差値を上げて合格を目指す. 更新日: 2022年4月30日. 公開日: 2021年8月24日. 基礎編・共通テスト対策. Tweet. 当サイトは、PRを含む場合があります。 上野竜生です。 今回は平方完成までできることを前提に,2次関数のグラフをかき,軸,頂点を求められることと,平行移動,対称移動までを扱います。 共通テストではこのレベルが問われますし,応用問題を解くときは絶対に必要な超基本事項です。 平方完成ができない人や復習したい人はこちらから復習しましょう。 2次関数の基礎 (平方完成) ここで間違えると大失点です. ath-juken.com/center/2jikansu1/ 上野竜生です。. 【応用】二次関数の決定(頂点がある直線上) | なかけんの . ここでは、ある二次関数のグラフの頂点がある直線上にあるときに、その二次関数を求める問題を考えます。 頂点に関する情報が与えられているので、 【基本】二次関数の決定(頂点・軸指定) で見たように、標準形で考えます。 📘 目次. 二 次 関数 の グラフ 頂点例題. おわりに. 例題. 二 次 関数 の グラフ 頂点ある二次関数のグラフが、放物線 y = x 2 を平行移動したもので、点 ( 1, 2) を通り、頂点が直線 y = 2 x − 3 上にあるとき、この二次関数を求めなさい。 頂点に関する情報があるので、まずはこれを利用するところから始めましょう。 標準形 y = a ( x − p) 2 + q の形で考えます。 頂点が y = 2 x − 3 上にある、という条件から、文字を1つ減らすことができます。. 平方完成のやり方4ステップ!二次関数のグラフの頂点がすぐ . 二 次 関数 の グラフ 頂点平方完成は、二次関数の頂点の座標を求めるときなど、数学の問題を解く過程で非常によく使います。 本記事では、 平方完成のやり方(4ステップ)を順を追って丁寧に解説 しています。 本記事を読み終える頃には、平方完成がスラスラできるようになっているでしょう。 ぜひ最後までお読みください! 【PR】勉強を効率的に継続して、志望校に合格したい方必見! ↓無料ダウンロードはこちら↓. 【目次】 1:平方完成のやり方. 2:平方完成の具体例. 1:平方完成のやり方. 平方完成とは、二次式ax2+bx+cを、a (x-p)2+qの形に変形すること です。 平方完成をすることで、二次関数の頂点の座標などを求めることができます。 では、どのようにして平方完成をすればよいのでしょうか?. 【基本】二次関数の決定(頂点・軸指定) - なかけんの数学ノート. 頂点や軸の条件が与えられている場合は、次の形で考えるとスムーズにいきます。 y = a ( x − p) 2 + q 頂点や軸を求めたいときにこの形に変形しましたが、逆に頂点や軸から二次関数を考えたいときも、この形を使うのがいいんですね。 (1)を考えてみましょう。 頂点が ( 1, 1) であることから、この二次関数は y = a ( x − 1) 2 + 1 であることがわかります。 つまり、頂点1点だけの情報で、「後は を求めれば終わり」というところまで進むんですね。 このグラフが ( 3, 5) を通るので、 5 = 4 a + 1 が成り立つことが分かります。 このことから、 a = 1 であることがわかります。. 【二次関数】頂点の求め方、公式は?問題を使ってイチから . 二 次 関数 の グラフ 頂点二次関数の頂点は、式を次のように表すことで求めることができます。 頂点 軸. では、二次関数の式を の形にするためには、どのような計算をしていけばよいのでしょうか。 次の二次関数を例に、平方完成のやり方を確認しておきましょう。 次の二次関数の頂点を求めなさい。 平方完成の手順. 二 次 関数 の グラフ 頂点の係数で、 と. 二 次 関数 の グラフ 頂点の項をくくってやります。. 超簡単!二次関数の頂点の求め方(平方完成と公式)2つを慶應 . 文頭でも述べた通り、 二次関数の頂点の求め方は2つあります。 1つは平方完成から求める方法、もう1つは二次関数の頂点の公式を暗記して求める方法です。 まずは平方完成から求める二次関数の頂点を求める方法について解説します。 実際に例題を解きながら理解していきましょう! 例題. 二 次 関数 の グラフ 頂点二次関数y=x 2 +6x+10の頂点の座標を求めよ。 解答&解説. 二次関数の頂点を求めるには、与えられた二次関数をまずは平方完成します。 ※平方完成のやり方を忘れてしまった人は、 平方完成について解説した記事 をご覧ください。 平方完成すると、 y. 二 次 関数 の グラフ 頂点=x 2 +6x+10. = (x+3)2+1. セラミック 歯 を 削る
木 やすり がけですね。 すると、二次関数y=x 2 +6x+10の頂点の座標は、. 二次関数の頂点とグラフの計算機. 二次関数の頂点とグラフ. 最大値・最小値 三次関数のグラフ. 二次関数の計算ツール | 頂点とグラフ. 本ツールは以下の計算結果を出力します。 ・頂点の座標. ・x軸との交点. 二 次 関数 の グラフ 頂点・二次関数のグラフ. 黄色い枠内の二次関数の係数 (large {a,b,c}) ( (large {a neq 0}))を入力し、『 計算実行 』を押してください。 【二次関数の設定】 二次関数 (large {y=ax^2+bx+c}) の係数. (large {a}) = (large {b}) = (large {c}) = 【出力値の設定】 出力値の小数点以下の桁数. 計算実行. 頂点の座標 (x,y) x軸との交点 (x,y). 二 次 関数 の グラフ 頂点2次関数の頂点の求め方 / 数学I by OKボーイ |マナペディア|. 2次関数の頂点の求め方. 二 次 関数 の グラフ 頂点「2次関数のグラフを描け」という問題がでてきたときに、まずやらなければならないことは グラフの頂点の座標を求めること です。 ここではその頂点の求め方について説明します。 y=x²+4x+6. 二 次 関数 の グラフ 頂点という2次関数があったとしましょう。 関数の式を変形する. 頂点を求めるにはまず、与えられた2次関数の式を. y=a (x+b)² +c. の形にすることから始めます。 因数分解のようにキレイな形にする必要はありません。 汚くても. y=a (x+b)² +c. の形にします。 今回の y=x²+4x+8 は、 y=x²+4x+8=x²+4x+4+4= (x+2)²+4. と変形することができます。 このとき「 (x+2) 」と「 +4 」に注目です。. 【標準】二次関数y=ax^2+bx+cのグラフの頂点 | なかけんの . 二次関数 y=ax^2+bx+c のグラフの頂点の求め方. 二次関数 y = a x 2 + b x + c のグラフをかくためには、まず頂点を求める必要がありました。 つまり、 y = a ( x − p) 2 + q の形に式変形をする必要がある、ということです。 このような式変形を行うことを「 平方完成 する」というんでしたね。 【標準】平方完成のやり方 では、具体的な数を含んだ式を変形していきましたが、ここでは文字のまま計算してみます。 まずは、 x 2 の係数でくくります。 + b x まででいい んでしたね。 y = a x 2 + b x + c = a ( x 2 + b a x) + c. 次が難しいところですが、カッコの部分を考えましょう。. 制約を持つ組合せ最適化問題を量子計算機で高精度に解くため . ウィンドウ を 並べて 表示 ショートカット
寝 てる 間 に 破水与えられたグラフの頂点集合を2個の部分集合に分割する問題。それぞれの部分集合に含まれる頂点の個数を等しくするという制約の下、異なる部分集合の間をつなぐ辺の数を最小にする組合せ最適化問題。 ※5 変分法 目的関数が最小 . 【基本】二次関数y=a(x-p)^2のグラフ | なかけんの数学ノート. 二 次 関数 の グラフ 頂点二次関数y=a (x-p)^2のグラフ. 例として、 y = x 2 のグラフを 軸方向に 1 だけ移動したものを考えてみます。. グラフは次のようになります。. グレーが移動前、黒い太線が移動後のグラフです。. 各点の移動に注目して、グラフを見ながら点の座標をいくつか . 二次関数のグラフと平方完成 - 高校数学.net. 二次関数の平方完成について学習するページです。平行完成のやり方だけでなく、何のために平方完成するのかということについても学習することができます。 . 二 次 関数 の グラフ 頂点次のグラフの頂点と軸の方程式を答え、グラフを図示せよ。 . 2次関数の公式と各単元を徹底解説!高校数学Ⅰ - マストラ高校数学まとめサイト. 定期テストに向けて2次関数の総復習がしたいです。. 本記事では 「2次関数の公式」や各単元を総復習 していきます。. 目次. 1 2次関数の公式まとめ. 2 そもそも2次関数とは?. 二 次 関数 の グラフ 頂点3 2次関数の頂点と軸の求め方. 4 2次関数のグラフの書き方. 5 平行移動させる公式 . 【基本】二次関数 y=ax^2 のグラフ | なかけんの数学ノート. 二次関数 y = a x 2 + b x + c について調べるためには、このグラフがかけた方がいいのですが、どうやってかけばいいのでしょうか。. まずは、 y = a x 2 の場合について、考えていくことにしましょう。. とてもシンプルな y = x 2 の場合を考えましょう。. a = 1 の . 【標準】二次関数と微分 | なかけんの数学ノート. 二 次 関数 の グラフ 頂点ここでは、微分の考えを使って、二次関数のグラフについて再度考えてみることにします。 すでに知っているものを再考するため、新しく問題が解けるようになるということはありませんが、微分の考えをより深めるために役立つと思います。. 二 次 関数 の グラフ 頂点学校では教わらない二次関数のグラフの書き方【書き直しを防ぐ】. 二次関数のグラフの書き方. 手順①:平方完成で頂点の「座標」「軸」を求める. 手順②: x 2 の係数を確認し「上凸」か「下凸」かを判断. 手順③:ここまでで分かったことを図に表す. 手順④:「頂点」と「y軸」の関係を図に書き込む. 手順⑤:「頂点」と . 二次関数 - Wikipedia. 定義. のことを x を独立変数とする 二次関数 という。. 二 次 関数 の グラフ 頂点特に b = c = 0 のときは、「二乗に比例する関数」とも言う。. 上記の標準形では、二次関数の 頂点 の座標は一般的に となる。. の形に表された二次関数を 一般形 (いっぱんけい、 standard form )という . 二 次 関数 の グラフ 頂点二次関数のグラフの書き方を徹底解説!!! - 理数白書. そしてグラフさえ理解していればあらゆる二次関数の問題が簡単に解けるようになります。. ここでは以下の問題を例にして、二次関数のグラフを描くために必要な全ての手順を徹底解説していきます。. 問題. 次の二次関数のグラフをかけ。. y = 2x2 − 12x + 14 . 二次関数の解き方、平方完成、グラフの本質が10分で理解できます! - 数検1級合格対策. この二次関数のグラフを書きましょう。. 二 次 関数 の グラフ 頂点平方完成は、次の3つのポイントで行います。. 逆に言えば、その3つのポイントさえおさえれば絶対に解けます。. 定数項以外を()でくくる. 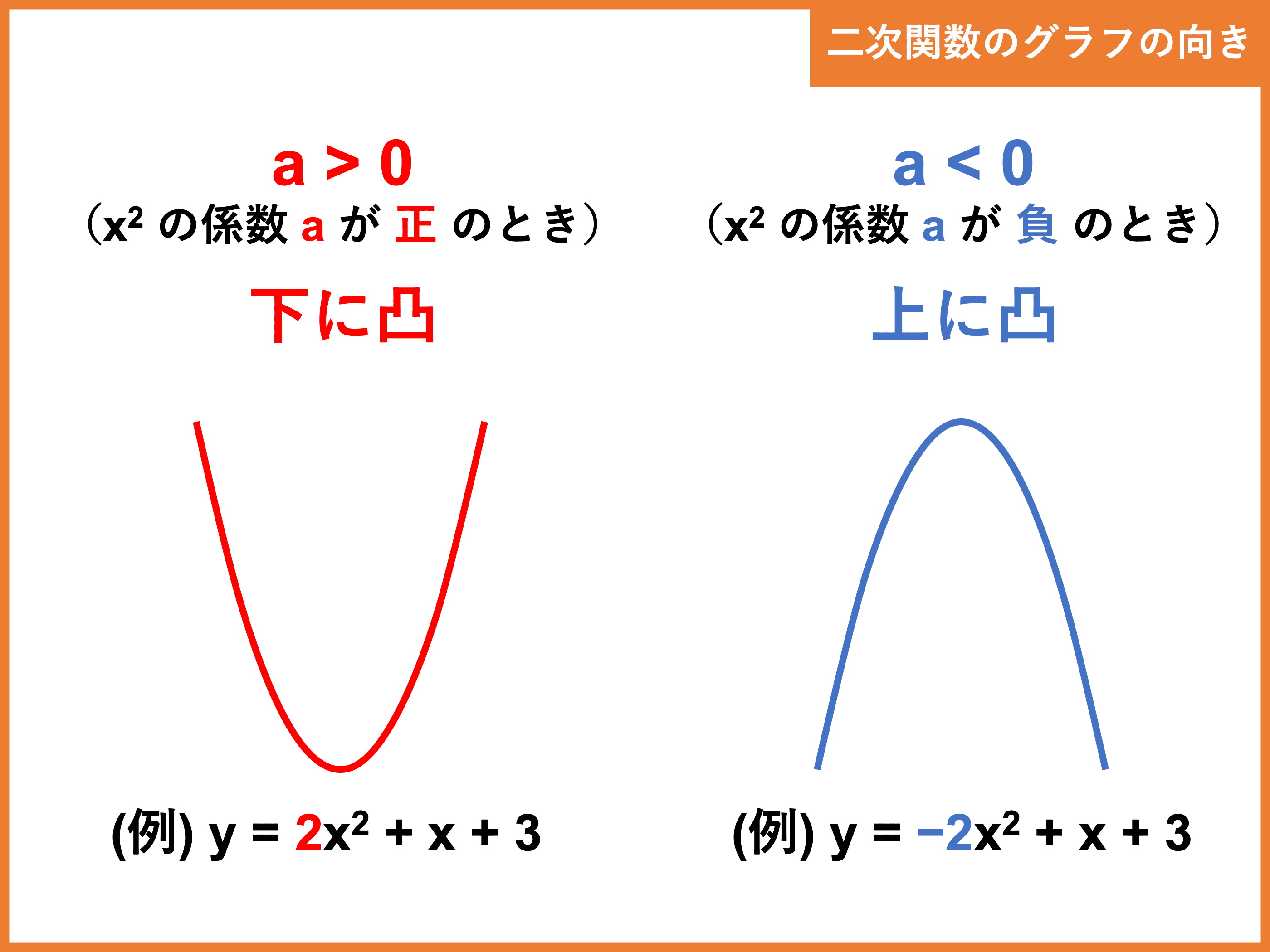
沖縄 県 教員 の 卵二次関数グラフの書き方を初めから解説! 二次関数の式の作り方をパターン別に解説! ←今回の記事; 二次関数を対称移動したときの式の求め方を解説! 平行移動したものが2点を通る式を作る方法とは? どのように平行移動したら重なる?. 二次関数の基本の解き方を押さえよう!練習問題の解説や勉強法も紹介|StudySearch. 二次関数のおすすめ勉強法. 二次関数のおすすめの勉強法は、基本を正確に理解し、焦らず落ち着いて何度も繰り返し練習することに尽きます。 特に平方完成は、その複雑な計算方法から、多くの高校生が挫折し、習得できなかった部分です。. 二 次 関数 の グラフ 頂点【高校 数学Ⅰ】 2次関数12 頂点と軸 (8分) - YouTube. 【この夏限定🌻無料学習相談】トライの個別指導が月8000円から受講可能!こんなお悩みはないですか?. 二次関数の式を決定する3つの型と4パターンを解説!. 二次関数の求め方は大きく分けると3つのタイプに分けることができます。 . 貸主 から の 解約 通知 書 書式
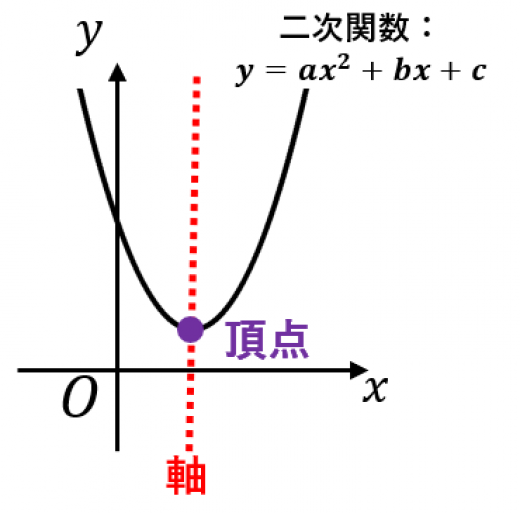
たんぽぽ 綿毛 に なる まで2次関数のグラフが3点(2,-2),(3,5),(-1,1)を通るとき、その2次関数を求めよう。 . 頂点の座標が(4,6)なので2次関数が以下の形をしていることが分かります。 . 軸・頂点【超わかる!高校数学Ⅰ・A】~授業~2次関数#3 - YouTube. 軸・頂点のポイントは!・ 2次関数のグラフは2次の係数が「+」だったら下に凸、「-」だったら上に凸の放物線になる!・ 2次の係数の絶対値が . 関数頂点計算機 - Symbolab. 無料の関数頂点計算機 - 関数の頂点をステップバイステップで求めます . 算術平均 幾何学的平均 二次 . ステップ グラフ . 二 次 関数 の グラフ 頂点二次関数のグラフの書き方. 次に、二次関数の係数aが正であることからグラフは下に凸なグラフとなりますので、頂点を基準に滑らかに下に凸な放物線を書きましょう。 不安な方は、頂点以外にも何点か通る場所を調べ、その点を通るような滑らかな曲線を書くことでより正確な . [数1]二次関数の頂点座標と軸を求める3つの方法【超簡単】. [数1]二次関数の頂点座標と軸を求める3つの方法【超簡単】 [数1]二次関数グラフの平行移動|わかりやすく具体例で解説 [数1]平方完成のやり方と平方完成の公式3つ|分数にも使える [数1]二次関数の最大値最小値の求め方を解説、定義域がある場合. 二 次 関数 の グラフ 頂点【標準】軌跡(放物線の頂点) | なかけんの数学ノート. 放物線の頂点の軌跡その1. 実数 が変化するとき、放物線 y = x 2 − 2 t x + t 2 + t + 1 の頂点の軌跡を求めなさい。. 頂点の軌跡なので、頂点の座標を求めないといけないですね。. 二 次 関数 の グラフ 頂点【標準】二次関数y=ax^2+bx+cのグラフの頂点 を参考にして、平方完成をすると. y = x . 2次関数の頂点の座標を計算します。 - 高精度計算サイト. 二 次 関数 の グラフ 頂点2次関数のグラフy=ax^2 +bx +c (aは0ではない)の頂点のx,y座標を計算します。 2次関数の頂点の座標を計算します。 - 高精度計算サイト. 2次関数のグラフの書き方 | おいしい数学. 2次関数のグラフの基本的な書き方. y = ax2 + bx+ c y = a x 2 + b x + c のグラフを書きます.. STEP1:平方完成して,頂点をうつ.. STEP2:都合のいい点 ( y y 切片が楽です)をうつ.. STEP3:うった点を通るように,放物線を意識して書く.. 二 次 関数 の グラフ 頂点 
指輪 pt950 とは二次関数の平行移動の問題を解く場合は、下図のように『 平行移動によって、頂点の位置がどのように変化するか 』と考えると分かりやすくなります。 【1-2】二次関数のグラフの一致. 次に、二次関数を平行移動させてグラフを一致させることを考えます。. 3点を通る二次関数の求め方!すぐに解ける裏ワザ2つもご紹介. a=2、b=5を②に代入して、c=1となります。. 二 次 関数 の グラフ 頂点よって求める二次方程式の式は y=2x2+5x+1 となります。. 以上が王道的な3点を通る二次関数の求め方です。. この求め方は必ず理解しておきましょう。. 上記のように、3点を通る二次関数の式を求める際にはy=ax 2 +bx+cの . 平方完成のやり方といくつかの発展形 | 高校数学の美しい物語. のように, 二次式 を a (x-p)^2+q a(x −p)2 +q の形に変形することを平方完成と言う。. 平方完成は,二次方程式の解の公式の導出や,二次関数のグラフを描くときに使う重要な式変形です。. 平 標 山 の 天気
エクセル 入力 したら 色 が 消える平方完成のやり方を基礎から説明します。. 目次. 平方完成の意味と . 2次関数[y=ax²+bx+cのグラフの頂点を求める方法] / 数学I by ふぇるまー |マナペディア|. 二 次 関数 の グラフ 頂点 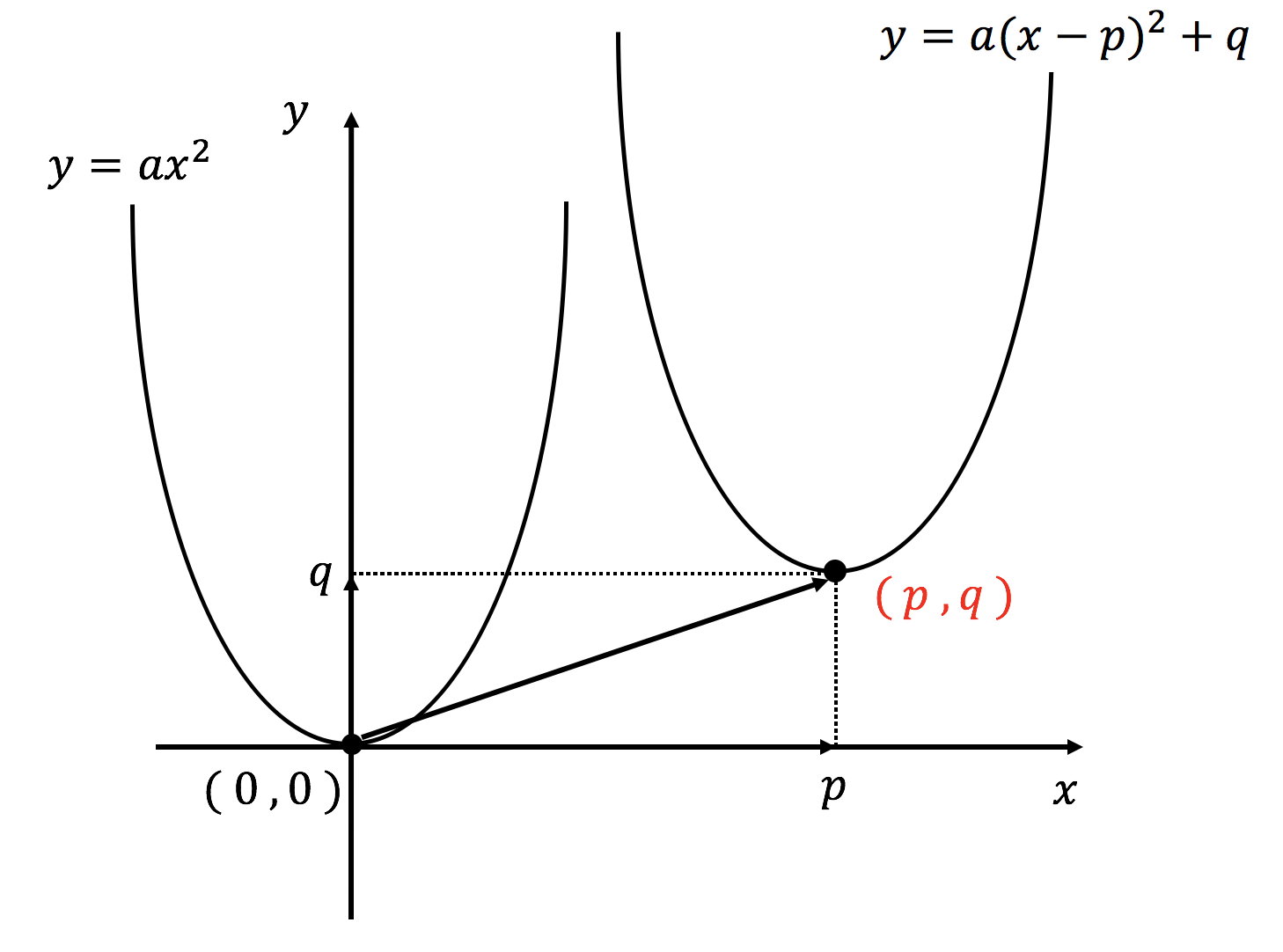
口 の 中 ヘルペス 画像数iで学ぶ二次関数の問題においてまず理解するべきなのは、軸・頂点の求め方です。二次関数を学ぶ方はみなさんぜひ理解して頂きたいところです。数学が苦手な方にも分かりやすい解説を心がけて記事を作りましたのでぜひご覧ください。. 都立 代々木 高校 偏差 値
【高校数学Ⅰ】「「頂点」をヒントに放物線の式を決める」 | 映像授業のTry IT (トライイット). 二 次 関数 の グラフ 頂点今回からは「放物線の式の決定」を学習していこう。. 第1回は 「『頂点』をヒントに放物線の式を決める」 のがテーマ。. 具体的には、こんな問題が出るよ。. 2次関数のグラフの頂点がわかっている状態から、式を求めにいくわけだね。. 頂点がわかって . 高校数学最初の難関 ― 2次関数の攻略法 | StudyGeek | スタディーギーク. 高校数学で最初に出会う難関といえば、2次関数です。2次関数はその後の三角関数や微分積分にもつながる重要な単元で、ここで躓くと高校数学全般が理解困難になってしまう可能性もあります。そんな大切な2次関数の攻略法を見てみましょう。2次関数の攻略のカギを一言で言うと、「正確な . 二 次 関数 の グラフ 頂点【基本】二次関数y=ax^2+qのグラフ | なかけんの数学ノート. 一般的に、次のことがいえます。. y = a x 2 + q のグラフ. y = a x 2 + q のグラフは、 y = a x 2 のグラフを y 軸方向に q だけ移動したものである. 二 次 関数 の グラフ 頂点【基本】二次関数 y=ax^2 のグラフ では、放物線の頂点と軸の紹介をしました。. 二 次 関数 の グラフ 頂点二次関数 y = a x 2 + q については、上の . 二 次 関数 の グラフ 頂点二次関数で頂点から式を求める方法を丁寧に解説!練習問題付き. 頂点の座標のみから二次関数の式を求めることは不可能なのでご注意ください。 例えば「頂点(1、2)を通る二次関数の式を求めよ」という問題があったとき、答えはy=x 2 +1やy=2x 2 など無数に存在してしまいます。.